Çoxluqlar nəzəriyyəsi

Anlayışlar

Hər hansı bir çoxluğu təşkil edən obyektlərə bu çoxluğun elementi deyilir. Çoxluqlar böyük hərflərlə, çoxluğun elementləri isə uyğun kiçik hərflərlə işarə olunur.

Çoxluq nəzəriyyəsində {displaystyle ain A} münasibəti o deməkdir ki, {displaystyle a} {displaystyle A} çoxluğunun elementidir. Bunun inkarı isə {displaystyle anotin A} kimi işarə edililirlər. Bu münasibət isə onu göstərir ki, {displaystyle a} {displaystyle A} çoxluğunun elementi deyil.

Alt Çoxluğu

 

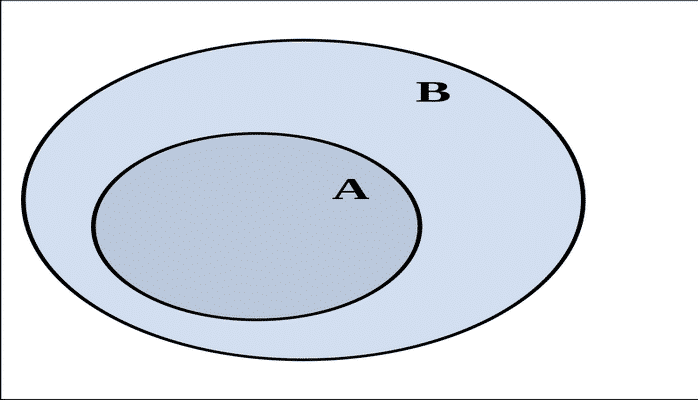
A çoxluğu B-nin altçoxluğudur

Bir çoxluq {displaystyle A} digər çoxluğun {displaystyle B} o vaxt altçoxluğu adlanır ki, {displaystyle A} çoxluğuna aid olan ixtiyari element həm də {displaystyle B} çoxluğunun elementi olsun.

{displaystyle B} o zaman {displaystyle A}-nin üstçoxluğu adlanır. Formal olaraq:

{displaystyle {A}subseteq {B}:Longleftrightarrow forall xleft({x}in Arightarrow xin Bright)}

.

Bərabərlik

İki çoxluq o zaman bərabərdirlər ki, onlar eyni elementlərə malik olsunlar.

Bu analyış çoxluq nəzəriyyəsinin əsası hesab olunur. Formal olaraq belə ifadə olunur:

{displaystyle A=B:Longleftrightarrow forall xleft(xin A,leftrightarrow xin Bright)}

Boş çoxluq

Tərkibində heç bir element olmayan çoxluq boş çoxluq adlanır. O {displaystyle emptyset } və ya {displaystyle {}} ilə işarə olunur. Bərabərlik qanunundan alınır ki, yalnız bir nir boş çoxluq mövcuddur. Digər boş çoxluqlar elə həmin elementləri əhatə edirlər, yəni bərabərdirlər. Uyğun olaraq: {displaystyle emptyset } və {displaystyle {emptyset }} müxtəlif olurlar. Çünki sonuncu çoxluq birincidən fərqli olan elementə sahibdir. Boş çoxluq hər bir çoxluğun alt çoxluğudur. Boş çoxluğu həmçinin aşağıdakı kimi də ifadə etmək olar:

{displaystyle emptyset _{A}={xin Amid forall xnotin A}}

{displaystyle emptyset _{A}} - A çoxluğunun boş alt çoxluğudur. Aşkar

Çoxluqların kəsişməsi

 

{displaystyle A} və {displaystyle B}-nin kəsişmə çoxluğu

A və B çoxluqlarının hər ikisinə eyni zamanda daxil olan bütün elementlərdən ibarət olan C çoxluğuna bu çox­luq­la­rın kə­siş­­mə­si deyilir:

Bir qeyri-xətti {displaystyle U} çoxluğu verilir. Bu çoxluqdan yaranmış kəsişmə çoxluğu A və B çoxluqlarına aid olan elemntlərdən təşkil olunur. Daha dəqiq desək, A və B çoxluqlarının kəsişməsindən yaranan çoxluğun elementləri, bu hər iki çoxluğun altçoxluğudur. Formal olaraq:

{displaystyle bigcap U:={xmid forall ain U:xin a}}

Çoxluqların birləşməsi

A və B çoxluqlarından heç olmasa birinə daxil olan bü­tün elementlərdən ibarət olan C çoxluğuna bu çoxluqların bir­ləşməsi de­­yi­lir və simvolik olaraq А U В kimi işarə olunur. Başqa sözlə, A və B çoxluqlarından birləşməsi nəticəsində alınan yeni C çoxluğunda hər iki çoxluğun bütünü elementləri daxildir. Çoxluqların birləşməsini rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5,6 rəqəmlərindən ibarətdir. Bu iki çoxluğun birləşməsi 1,2,3,4,5,6 rəqəmindən ibarət yeni çoxluq olacaq, çünki 3 və 4 rəqəmləri A çoxluğunda da, B çoxluğunda da var və tam olaraq həm A, həmdə B çoxluğu nəticədə alınan çoxluğa daxildir. Əgər А={1,2,3,4}, B={3,4,5,6}, onda A U B = {1,2,3,4,5,6}:A və B çoxluqlarından heç olmasa birinə daxil olan bü­tün elementlərdən ibarət olan C çoxluğuna bu çoxluqların bir­ləşməsi de­­yi­lir və simvolik olaraq А U В kimi işarə olunur. Başqa sözlə, A və B çoxluqlarından birləşməsi nəticəsində alınan yeni C çoxluğunda hər iki çoxluğun bütünü elementləri daxildir. Çoxluqların birləşməsini rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5,6 rəqəmlərindən ibarətdir. Bu iki çoxluğun birləşməsi 1,2,3,4,5,6 rəqəmindən ibarət yeni çoxluq olacaq, çünki 3 və 4 rəqəmləri A çoxluğunda da, B çoxluğunda da var və tam olaraq həm A, həm də B çoxluğu nəticədə alınan çoxluğa daxildir. Əgər А={1,2,3,4}, B={3,4,5,6}, onda A U B = {1,2,3,4,5,6}:

{textstyle bigcap U:={xmid forall xnotin A}}.

 

{displaystyle A} və  {displaystyle B} çoxluqlarından yaranmış birləşim çoxluğu